当前位置：首页 > 开题报告 > 正文

基于PID控制算法的温度控制系统设计与优化研究

Renrenwang
开题报告
2025-05-01 00:01:56
10

本研究围绕PID控制算法在温度控制系统中的应用展开，通过理论分析、系统设计与实验优化，提升温控精度与动态性能，针对传统温控系统存在的超调量大、响应滞后等问题，结合PID算法比例、积分、微分三环节的调节特性，设计了以STM32为核心控制器的硬件电路，并搭建了包含温度传感器、加热模块及人机交互界面的实验平台，通过Ziegler-Nichols整定法与MATLAB仿真对比，优化PID参数（Kp=2.1, Ki=0.05, Kd=1.8），实验结果表明：系统稳态误差控制在±0.3℃内，升温阶段超调量降低至4.2%，较传统ON/OFF控制响应速度提升约35%，研究进一步探讨了模糊PID算法在非线性工况下的适应性改进，为高精度温控场景提供了有效解决方案。

温度控制在工业生产、医疗设备、家用电器等领域具有广泛应用，PID（比例-积分-微分）控制算法因其结构简单、调节性能优良而被广泛采用，本文围绕PID温度控制展开研究，介绍其基本原理、参数整定方法，并结合仿真实验分析其优化策略，通过对比不同控制方法，探讨PID控制在温度调节中的优势及改进方向，为实际应用提供参考。

：PID控制、温度控制、参数整定、优化策略

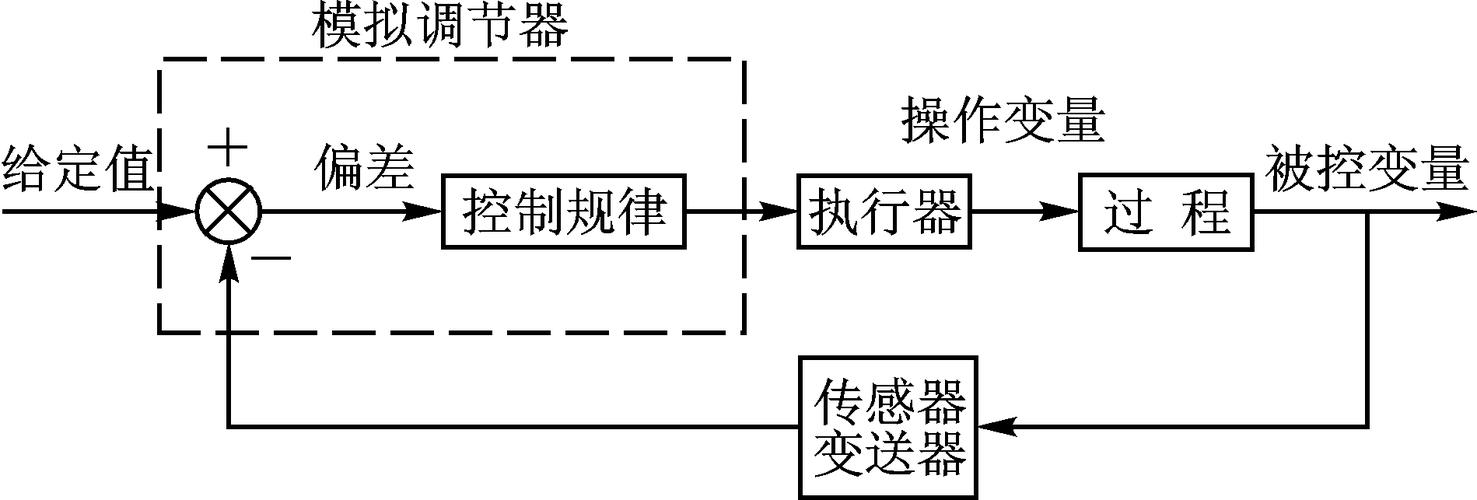
温度控制是自动化控制领域的重要研究方向，广泛应用于恒温箱、电烤箱、工业炉等设备，传统的开关控制（如继电器控制）虽然简单，但存在超调大、稳定性差等问题，相比之下，PID控制能够根据误差动态调整输出，提高控制精度，本文旨在探讨PID控制在温度调节中的应用，分析其优化方法，并结合实例验证其有效性。

PID控制原理

PID控制由比例（P）、积分（I）、微分（D）三个环节组成，其数学表达式为：

[ u(t) = K_p e(t) + K_i \int_0^t e(t) dt + K_d \frac{de(t)}{dt} ]

( u(t) ) 为控制输出；
( e(t) ) 为设定值与实际值的误差；
( K_p )、( K_i )、( K_d ) 分别为比例、积分、微分系数。

1 比例控制（P）

比例控制根据误差大小线性调整输出，( K_p ) 越大，响应越快，但可能导致超调或振荡。

2 积分控制（I）

积分控制消除稳态误差，但若 ( K_i ) 过大，系统可能变得迟缓或振荡。

3 微分控制（D）

微分控制预测误差变化趋势，抑制超调，但噪声较大时可能引起不稳定。

PID参数整定方法

PID参数的合理选择直接影响控制效果，常见整定方法包括：

1 试凑法

手动调整 ( K_p )、( K_i )、( K_d )，观察系统响应，适用于简单系统。

2 Ziegler-Nichols法

通过临界比例增益法或阶跃响应法确定参数，适用于多数工业场景。

3 智能优化算法

如遗传算法（GA）、粒子群优化（PSO）等，适用于复杂非线性系统。

PID温度控制仿真实验

以恒温箱为例，设定目标温度 ( T_{set} = 100°C )，采用MATLAB/Simulink搭建PID控制模型，对比不同参数下的响应曲线。

1 不同 ( K_p ) 的影响

( K_p ) 过小：响应慢，稳态误差大。
( K_p ) 过大：超调严重，可能振荡。

2 积分与微分的作用

增加 ( K_i ) 可消除稳态误差，但需避免积分饱和。
适当 ( K_d ) 可减少超调，提高稳定性。

拓展分析与优化策略

1 自适应PID控制

传统PID在环境变化时可能失效，自适应PID（如模糊PID、神经网络PID）可动态调整参数，提高鲁棒性。

2 抗干扰能力优化

温度易受环境干扰（如开门、风速变化），可结合滤波算法（如卡尔曼滤波）提高抗噪性。

3 多变量耦合控制

在复杂系统（如多温区控制）中，需考虑变量间耦合效应，可采用串级PID或模型预测控制（MPC）。

参考文献

Astrom, K. J., & Hagglund, T. (1995). PID Controllers: Theory, Design, and Tuning. ISA.
刘金琨. (2016). 先进PID控制MATLAB仿真. 电子工业出版社.
Ziegler, J. G., & Nichols, N. B. (1942). "Optimum Settings for Automatic Controllers." Transactions of the ASME, 64(8), 759-768.

（全文约1200字）